สัจพจน์ของกลศาสตร์ควอนตัม (Axioms of Quantum Mechanics)

สุวิทย์ กิระวิทยา

13 กุมภาพันธ์ 2561

สัจพจน์ของกลศาสตร์ควอนตัมจะแสดงเป็นข้อความสั้น ๆ เพียงไม่กี่ข้อ (4 ข้อในที่นี้) ที่ใช้เป็นเสมือนกฎในการศึกษาทำความเข้าใจการอธิบายปรากฎการณ์ต่าง ๆ ที่สังเกตและวัดได้จริงด้วยกลศาสตร์ควอนตัม

โดยก่อนที่จะกล่าวถึงสัจพจน์เหล่านี้ เราจะต้องกำหนดความสัมพันธ์ระหว่างปริมาณทางฟิสิกส์และรูปแบบวัตถุทางคณิตศาสตร์ที่นำมาใช้อธิบายเสียก่อน โดยสำหรับกลศาสตร์ควอนตัมนั้น เราใช้ความรู้เรื่องเวกเตอร์ปริภูมิ (ในพีชคณิตเชิงเส้น) เป็นพื้นฐาน โดยมีข้อกำหนดคือ

1. สถานะของระบบทางกายภาพจะแสดงได้ด้วยเวกเตอร์สถานะในปริภูมิฮิลเบิร์ท H (Hilbert space) ซึ่งหมายความว่าเวกเตอร์* |yñ และ l|yñ (โดยที่ l ¹ 0) แทนสถานะเดียวกัน โดยทั่วไปแล้วเราจะสมมติให้เวกเตอร์สถานะนี้ถูกนอร์มัลไรซ์แล้ว (áy |yñ = 1 )

2. ตัวแปรพลวัตที่สามารถตรวจวัดได้ในระบบทางกายภาพจะแสดงด้วย "ตัวดำเนินการที่สังเกตได้" (observable operator) ในปริภูมิ H ซึ่งหมายความว่าตัวดำเนินการนี้มีคุณสมบัติเฮอร์มิเทียน (Hermitian) โดยตัวดำเนินการนี้มีเวกเตอร์เจาะจงที่สามารถใช้เป็นเวกเตอร์ฐานในการเขียนเวกเตอร์ใด ๆ ในปริภูมิ H ได้

* สำหรับในวิชากลศาสตร์ควอนตัมนี้ เราจะใช้สัญลักษณ์เค็ท (ket) |.ñ แทนเวกเตอร์ โดยเรียกการเขียนรูปแบบนี้ว่า สัญกรณ์บรา-เค็ทของดิแรก (Dirac bra-ket notation)

สัจพจน์ 4 ข้อ ของกลศาสตร์ควอนตัม มีดังนี้

สัจพจน์ 1: ผลการวัดที่เกิดขึ้นได้ (จากการวัดปริมาณใด ๆ ที่ตรวจวัดได้ในระบบ) จะเป็นได้เพียงค่าเจาะจงตัวหนึ่งของตัวดำเนินการที่สอดคล้องกับการวัดนั้น โดยผลจากการกระทำการวัดนี้ทำให้ระบบเปลี่ยนไปอยู่ในสถานะที่แสดงได้ด้วยเวกเตอร์เจาะจงที่สอดคล้องกับค่าเจาะจงที่วัดได้

สัจพจน์ 2: ถ้าหากเราทราบว่าระบบอยู่ในสถานะ |A'ñ แล้ว ความน่าจะเป็นที่การวัด B จะให้ค่าเป็น B' คือ

P(A',B') = |áA' | B'ñ|² (1-1)

โดยถ้าหากว่า B เป็นการวัดที่มีความต่อเนื่อง จะได้ว่า

|áA' | B'ñ|² dB' (1-2)

คือความน่าจะเป็นของการวัด B จะให้ค่าอยู่ในช่วง B' ถึง B' + dB'

สัจพจน์ 3: ตัวดำเนินการ A และ B จะสอดคล้องกับตัวแปรพลวัตแบบดั้งเดิม A และ B ที่สอดคล้องกับความสัมพันธ์ไปกลับ (commutation relation)

[A, B] = AB – BA = iħ{A, B}_op (2)

โดย { , }_op คือตัวดำเนินการที่สอดคล้องกับบราคเค็ทปัวซงแบบดั้งเดิม (Poisson bracket) คือ

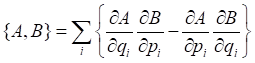(3)

โดยที่ p_i และ q_i คือพิกัดและโมเมนตัมของระบบ (ที่นิยามแบบดั้งเดิม กลศาสตร์คลาสสิก) ซึ่งจากความสัมพันธ์คอมมูทเทชันนี้เราแสดงให้เห็นโดยง่ายได้ว่า

[q_i, q_j] = [p_i, p_j] = 0 (4-1)

และ [q_i, p_i] = iħ d_ij 1 (4-2)

โดย d_ij คือโครเนคเกอร์เดลต้า (Kronecker delta) มีค่าเท่ากับหนึ่งเมื่อ i เท่ากับ j และเท่ากับศูนย์เมื่อ i และ j ไม่เท่ากัน

สัจพจน์ข้อ 3 นี้นำมาซึ่งการค้นพบที่สำคัญคือ ถ้าหากเรานิยามค่าคาดคะเน (expectation value) ของสิ่งที่สังเกตได้ด้วย

áAñ = á y | A | y ñ (5)

และนิยามความไม่แน่นอน (uncertainty) ด้วย

DA = á (A - 1 áAñ)² ñ^1/2 (6)

เราจะสามารถแสดงให้เห็น (โดยใช้อสมการชวาส (Schwarz's inequality)) ได้ว่า

(DA²) (DB²) ³ -1/4á [A, B] ñ² (7)

ซึ่งหากแทน A ด้วย p_i และ B ด้วย q_j และใช้สมการ (4-2) จะได้ความสัมพันธ์ความไม่แน่นอนของไฮเซนเบิร์ก (Heisenberg uncertainty) คือ

Dp_i Dq_j ³ (ħ/2) d_ij (8)

ถึงตรงนี้ เรากล่าวถึงเพียงแค่ความเชื่อมโยงกันระหว่างเวกเตอร์และสิ่งที่สังเกตได้ ณ เวลาหนึ่ง สำหรับพลวัตของระบบนั้นเราสามารถจำลองได้หลายวิธี ซึ่งแต่ละวิธีจะผลลัพธ์ที่สอดคล้องกัน โดยสำหรับสัจพจน์ข้อสุดท้ายนี้เราจะนำเสนอ ภาพของชโรดิงเจอร์ (Schrödinger picture) หรือเรียกว่า การนำเสนอแบบชโรดิงเจอร์ ซึ่งมีรูปแบบคือ เวกเตอร์สถานะจะเป็นฟังก์ชันของเวลาและตัวดำเนินการที่สังเกตได้จะไม่ขึ้นกับเวลา

สัจพจน์ 4: กำหนดให้สถานะของระบบที่เวลา t₀ คือ |y₀ñ และสถานะของระบบที่เวลา t ใด ๆ คือ |yñ สถานะทั้งสองนี้จะสัมพันธ์กันด้วยการแปลงยูนิแทรี (unitary transformation) คือ

|yñ = U(t – t₀) |y₀ñ (9)

โดยที่

U(t – t₀) = exp(-i/ħ H(t – t₀)) (10)

และ H คือตัวดำเนินการฮามิลโทเนียน (Hamiltonian operator) ซึ่งแทนพลังงานรวมของระบบ

หากกำหนดให้ t –t₀ = dt, |yñ – |y₀ñ = d |yñ และ

U(dt) = exp(-i/ħ H dt) = 1 – i/ħ H dt (12)

จะได้ว่า

(13)

ซึ่งสมการนี้มีชื่อเรียกว่า สมการชโรดิงเจอร์

แนวทางอธิบายพลวัตของระบบที่เทียบเท่ากับภาพของชโรดิงเจอร์ คือ ภาพของไฮเซนเบิร์ก (Heisenberg picture) ซึ่งกำหนดให้ U = U(t – t₀) และพิจารณาการแปลงยูนิแทรีคือ

|yñ_H = U^-1|yñ_S = U^-1 U |y₀ñ_S = |y₀ñ_S (14)

และ A_H(t) = U_t^-1A_SU_t (15)

โดยตัวห้อย S และ H บ่งบอกสถานะและตัวดำเนินการในภาพของชโรดิงเจอร์และไฮเซนเบิร์กตามลำดับ ซึ่งในภาพของไฮเซนเบิร์กนี้ เวกเตอร์สถานะจะคงที่ในขณะที่ตัวดำเนินการ A_H จะขึ้นกับเวลา คือ

(16)

โดยการเขียนแสดงอนุพันธ์ของ A_H จะได้ว่า

(17)

ซึ่งสมการนี้มีชื่อเรียกว่า สมการการเคลื่อนที่ของไฮเซนเบิร์กสำหรับตัวดำเนินการ A_H โดยสมการการเคลื่อนที่นี้สามารถเทียบเคียงได้กับสมการการเคลื่อนที่แบบดั้งเดิมสำหรับตัวแปรพลวัตในรูปแบบบราคเค็ทปัวซง คือ

(18)

โดยจากสมการ (17) จะพบว่าตัวดำเนินการที่ไปกลับได้ (commute) กับฮามิลโทเนียนจะแสดงการเคลื่อนที่แบบคงที่

เอกสารอ้างอิง

[1] E. G. Harris, A Pedestrain Approach to Quantum Field Theory, John Wiley & Sons (1972)

[2] https://en.wikipedia.org/wiki/Mathematical_formulation_of_quantum_mechanics

End