สูตรคณิตศาสตร์พื้นฐาน
(Basic Mathematical Formula)

สุวิทย์ กิระวิทยา

26 เมษายน 2562

1. ค่าคงที่และพหุนาม

1.1 ค่าคงที่ (constant)

1.1.1

1.1.2

1.1.3

1.1.4

โดย เป็นเลขฐานธรรมชาติ

1.1.5

1.1.6

1.1.7

1.1.8

1.1.9

1.1.10

1.1.11

โดย คือค่าคงที่ออยเลอร์ (Euler’s constant)

1.1.12

โดย คือสัดส่วนทอง (golden ratio)

1.1.13

โดย อ่านว่า องศา (degree) และ อ่านว่า เรเดียน (radian)

1.1.14

1.1.15

ทุกจำนวนที่แสดงในหน้านี้เป็นจำนวนอตรรกยะ (irrational number)

1.2 การแยกตัวประกอบ (factorization)

1.2.1

1.2.2

1.2.3

1.2.4

1.2.5

1.2.6

1.2.7

1.2.8

1.2.9

1.2.10

1.2.11

1.2.12

1.2.13

1.2.14

1.2.15

1.2.16

1.2.17

1.2.18

1.2.19

เมื่อ เป็นจำนวนคี่

1.2.20

เมื่อ เป็นจำนวนคี่

1.3 สัมประสิทธิ์ทวินาม (binomial coefficient)

แฟกทอเรียล (factorial)

1.3.1

โดยกำหนดให้

สูตรทวินาม (binomial formula)

1.3.2

หรือ

1.3.3

โดยสัมประสิทธิ์ทวินาม (binomial coefficient) คือ

1.3.4

โดย

เช่น , ,

และ

ตัวอย่างเช่น เรากระจาย ได้ โดยให้ และ

จะได้ว่า

และ

และจะได้ว่า

คุณสมบัติของสัมประสิทธิ์ทวินาม

1.3.5

1.3.6 ()

1.3.7

1.3.8

1.3.9

1.3.10

1.3.11

1.3.12

1.3.13

1.4 รากของสมการ (root of algebraic equations)

สมการกำลังสอง (quadratic equation): โดยที่

มีผลเฉลย (ราก) คือ

1.4.1

ผลเฉลยแบ่งได้ 3 กรณี ขึ้นกับ ที่เรียกว่าค่าดิสคริมิแนนต์ (discriminant) คือ

กรณี (1) จะได้ว่า ผลเฉลยเป็นจำนวนจริง 2 ค่าที่มีค่าไม่เท่ากัน

กรณี (2) จะได้ว่า ผลเฉลยเป็นจำนวนจริง 2 ค่าที่มีค่าเท่ากัน

กรณี (3) จะได้ว่า ผลเฉลยเป็นจำนวนเชิงซ้อน 2 ค่า ที่เป็นค่าสังยุคเชิงซ้อน (complex conjugate)

หากให้ และ คือผลเฉลยของสมการกำลังสอง และ จะมีคุณสมบัติคือ

1.4.2 และ

สมการกำลังสาม (cubic equation): โดยที่

กำหนดให้

,

และ

ผลเฉลยของสมการกำลังสามคือ

1.4.3

โดยที่

, และ

ค่าดิสคริมิแนนต์ หาได้จาก

1.4.4

ผลเฉลยแบ่งได้ 3 กรณี ขึ้นกับค่าดิสคริมิแนนต์ คือ

กรณี (1) จะได้ว่า ผลเฉลยเป็นจำนวนจริง 3 ค่าที่มีค่าไม่เท่ากัน

กรณี (2) จะได้ว่า ผลเฉลยเป็นจำนวนจริง 3 ค่า ที่มีอย่างน้อยสองค่ามีค่าเท่ากัน

กรณี (3) จะได้ว่า ผลเฉลยเป็นจำนวนจริง 1 ค่าและจำนวนเชิงซ้อน 2 ค่าที่เป็นค่าสังยุคเชิงซ้อน

ผลเฉลยของสมการกำลังสามมีคุณสมบัติคือ

1.4.5

และ

2. เรขาคณิตสองมิติ

2.1 สูตรที่เกี่ยวกับรูปทรงสองมิติ (geometric formula)

สี่เหลี่ยมผืนผ้า (rectangle) มีความกว้าง และความยาว

2.1.1 เส้นรอบรูป (perimeter, )

2.1.2 พื้นที่ (area, )

รูปที่ 2.1 สี่เหลี่ยมผืนผ้า

สี่เหลี่ยมด้านขนาน (parallelogram) มีความสูง และฐานยาว

2.1.3 เส้นรอบรูป

2.1.4 พื้นที่

รูปที่ 2.2 สี่เหลี่ยมด้านขนาน

สามเหลี่ยม (triangle) มีความสูง และฐานยาว

2.1.5 เส้นรอบรูป

2.1.6 พื้นที่

โดยที่

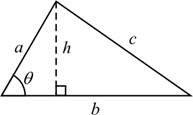
รูปที่ 2.3 สามเหลี่ยม

สี่เหลี่ยมคางหมู (trapezoid) มีความสูง และด้านที่ขนานกันยาว และ

2.1.7 เส้นรอบรูป

2.1.8 พื้นที่

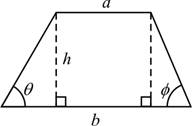
รูปที่ 2.4 สี่เหลี่ยมคางหมู

วงกลม (circle) มีรัศมี หรือเส้นผ่านศูนย์กลาง

2.1.9 เส้นรอบวง (circumference, )

2.1.10 พื้นที่

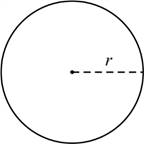
รูปที่ 2.5 วงกลม

สามเหลี่ยมฐานโค้ง (sector of circle) รัศมี มุมรองรับฐาน

2.1.11 เส้นรอบรูป

2.1.12 พื้นที่ ( ในหน่วยเรเดียน)

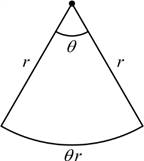
รูปที่ 2.6 สามเหลี่ยมฐานโค้ง

ส่วนของวงกลม (segment of circle) รัศมี

2.1.13 เส้นรอบรูป

2.1.14 พื้นที่

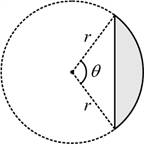
รูปที่ 2.7 ส่วนของวงกลม

รูปหลายเหลี่ยมด้านเท่า (regular polygon) มี ด้านและความยาวแต่ละด้าน

2.1.15 เส้นรอบรูป

2.1.16 พื้นที่

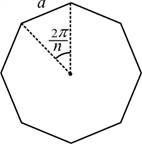
รูปที่ 2.8 รูปหลายเหลี่ยมด้านเท่า

วงรี (ellipse)

ที่มีความยาวครึ่งแกนเอก (major axis) และความยาวครึ่งแกนโท (minor axis)

2.1.15 เส้นรอบรูป (โดยประมาณ)

โดยที่

2.1.16 พื้นที่

2.1.17 ความเยื้องศูนย์กลาง (eccentricity)

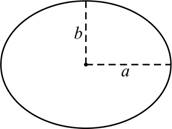
รูปที่ 2.9 วงรี

2.2 ระบบพิกัดฉาก (Cartesian coordinate)

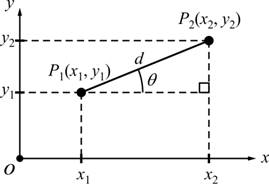
รูปที่ 2.10 จุดสองจุดในระบบพิกัดฉากสองมิติ

ระยะห่างระหว่างจุด และ

2.2.1

ความชันของเส้นที่เชื่อมต่อจุด และ

2.2.2

สมการเส้นตรงของเส้นที่เชื่อมต่อจุด และ

2.2.3

หรือ

2.2.4

โดยที่ คือระยะตัดแกน (y-intercept)

สมการเส้นตรงที่แสดงในรูปแบบของระยะตัดแกน และ

2.2.5 (โดยที่ และ )

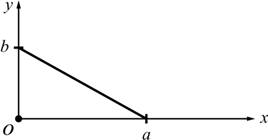
รูปที่ 2.11 เส้นตรงในระบบพิกัดฉากสองมิติ

สมการเส้นตรงในรูปแบบทั่วไป

2.2.6

ระยะห่างระหว่างจุด และเส้นตรง

2.2.7

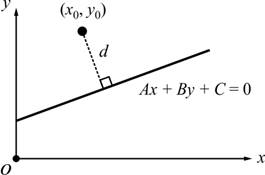
รูปที่ 2.12 ระยะห่างระหว่างจุดกับเส้นตรง

มุมระหว่างเส้นตรงสองเส้นที่มีความชัน และ

2.2.7

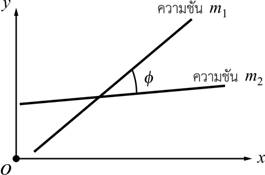
รูปที่ 2.13 มุมระหว่างเส้นตรงสองเส้น

เส้นตรงสองเส้นที่มีความชัน และ จะขนานกัน (parallel) ก็ต่อเมื่อ

2.2.8

เส้นตรงสองเส้นที่มีความชัน และ จะตั้งฉากกัน (perpendicular) ก็ต่อเมื่อ

2.2.9

พื้นที่สามเหลี่ยม ที่มีจุดยอดอยู่ที่ , และ

2.2.10

โดย คือค่าดีเทอร์มิแนนต์ (determinant) และเลือกเครื่องหมายบวกลบเพื่อให้ได้ค่าพื้นที่เป็นบวกเสมอ

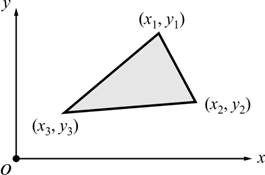
รูปที่ 2.14 สามเหลี่ยมที่มีจุดยอดอยู่ที่ , และ

การเลื่อนแกน (pure translation of coordinate)

2.2.11

โดย คือจุดกำเนิด (origin) ของแกนใหม่ () ที่เลื่อนไปจากแกน เดิม

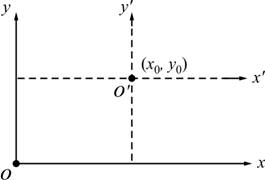
รูปที่ 2.15 การเลื่อนแกน

การหมุนแกน (pure rotation of coordinate)

2.2.12

โดย คือมุมที่หมุนไปจากแกน เดิม

รูปที่ 2.16 การหมุนแกน

สมการวงกลมรัศมี จุดศูนย์กลางอยู่ที่

2.2.13

หรือ

2.2.14

โดยที่ และ

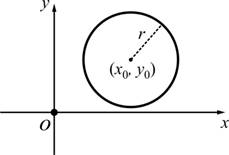
รูปที่ 2.17 วงกลม

พาราโบลา (parabola) มีจุดยอดอยู่ที่

2.2.15

หรือ

2.2.16

โดยที่ คือระยะห่างจากจุดยอดถึงจุดโฟกัส (focus) , และเครื่องหมายของ กำหนดลักษณะพาราโบลา หาก จะเป็นพาราโบลาหงาย

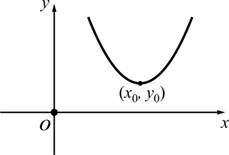
รูปที่ 2.18 พาราโบลาหงาย

วงรีมีจุดศูนย์กลางอยู่ที่ มีความยาวครึ่งแกนเท่ากับ และ

2.2.17

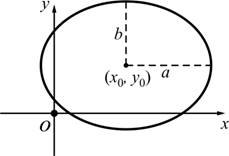
รูปที่ 2.19 วงรี

ไฮเปอร์โบลา (hyperbola) มีจุดศูนย์กลางอยู่ที่ มีความยาวครึ่งแกนเท่ากับ และ

2.2.18

หรือ

2.2.19

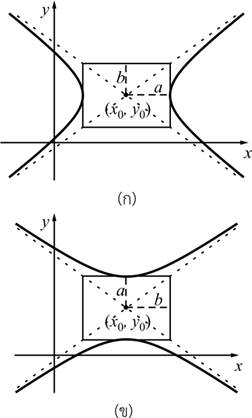
รูปที่ 2.20 ไฮเปอร์โบลา (ก) แกนหลักตามนอน และ (ข) แกนหลักตามตั้ง

2.3 ระบบพิกัดเชิงขั้ว (polar coordinate)

การแปลงระหว่างระบบพิกัดฉากและระบบพิกัดเชิงขั้ว

2.3.1 2.3.2

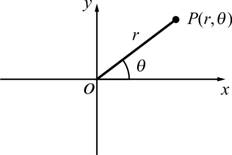
รูปที่ 2.21 ระบบพิกัดฉากและระบบพิกัดเชิงขั้ว

สมการวงกลมรัศมี จุดศูนย์กลางอยู่ที่จุดกำเนิด

2.3.3

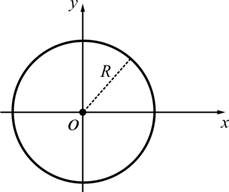
รูปที่ 2.22 วงกลมที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิด

สมการวงกลมรัศมี จุดศูนย์กลางอยู่ที่จุด

2.3.4

หรือ

2.3.5

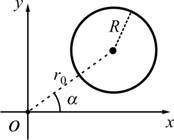
รูปที่ 2.23 วงกลมที่มีจุดศูนย์กลางอยู่ที่จุด

สมการเส้นตรงที่ผ่านจุดกำเนิด

2.3.6

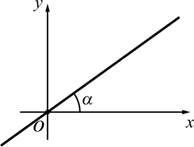
รูปที่ 2.24 เส้นตรงที่ผ่านจุดกำเนิด

ภาคตัดกรวย (conic section)

2.3.7

โดย คือความเยื้องศูนย์กลาง (ดู (2.1.17))

สมการวงกลมจะมี

สมการวงรีจะมี

สมการพาราโบลาจะมี

สมการไฮเปอร์โบลาจะมี

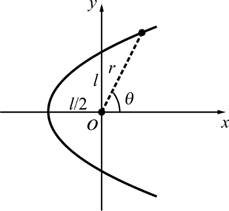
รูปที่ 2.25 พาราโบลาตะแคงขวา

ดูเหมือนว่า เนื้อหาตามหัวข้อของเอกสารนี้ จะไม่มีที่สิ้นสุด แต่ผู้เขียนขอสิ้นสุดการบันทึกนี้ ไว้ ณ ที่นี้

End